Contents
- What is ICM?
- Why ICM Poker is important
- How ICM works
- When does ICM factor in tournaments?
- ICM and final table deals
- The limitations of ICM
- How to develop your ICM skill
What is ICM?
ICM stands for the Independent Chip Model. It is a model that allows you to convert a tournament players chips into their real money equity as a percentage of the total prize pool. It essentially allows you to get a real money value for your tournament chip stack or to work out the financial risk/reward of a particular decision in tournaments. If you play tournaments it is essential you have a knowledge of ICM poker, otherwise you will make big financial mistakes.
Before it was known as ICM, the Independent Chip Model began life as the Malmuth-Harville Formula in 1987. It was based on a similar formula for making horse racing predictions and was initially used in poker to get an estimate of the value of a stack at a final table for deal making purposes. It was much later after the online poker boom that ICM was used to guide strategic decisions. In particular the decisions on or around the money bubble, and afterwards.
The early adopters of ICM were mostly Sit & Go (SNG) grinders because single table tournaments were much easier to ‘solve’ in ICM spots because they had a small amount of players. SNG grinders were also exposed to more situations where ICM had a major influence in any given session every time they played. ICM fell out of fashion for a while when multi table tournaments became the dominant format in online poker, but in recent years MTT grinders have woken up to the importance of ICM in large field tournaments.
ICM being adopted by SNG grinders led to the creation of ICM solver technology like ICMIZER which has developed and kept up with the changing landscape of online poker. ICM applies to all poker formats where there are two or more payouts, whether they are MTTs, PKOs, satellites, SNGs, Double or Nothings, Spin & Go Max, or anything else that is developed in the future of poker.
Why ICM Poker is important
In a cash game the value of a poker chip is constant. A $1 chip represents $1 at the tables at all times. In a tournament that is not the case, the value of your chips fluctuate throughout the game. As such your decisions in a tournament are different to a cash game, even if the position, cards and number of blinds are identical. If you play a tournament hand exactly like you would a cash game hand you will lose a lot of money over time.
A good way to grasp why ICM is one of the most important considerations in poker tournaments is with a simple example. Let’s say you are playing in a $100 SNG with ten players and there is no rake. Each player begins with 100 chips. What is the value of a single chip at the start of the tournament?
The answer is $1. There are 100 chips, one for every dollar of the buy-in.
Let’s say that this tournament has three payouts - $500 for 1st, $300 for 2nd and $200 for third. Each player at the table has eliminated another player at the table, meaning five players remain and they all have 200 chips each. What is the value of a single chip now?
It is still $1. Each player has 200 chips and essentially has $200 of equity now, so each chip is worth $1.
Now let’s fast forward to the end of the tournament and one player, let’s call her Jane, has won all the chips, so she has 1,000 chips. What is the value of a single chip in her stack now?
The answer is actually $0.50.
What has happened?
The chips have literally halved in value. This is because of what separates tournaments from cash games - the payouts. Jane has won $1,000 worth of chips but because of the payouts she can only win the first prize of $500. If this had been a $100 buy-in cash game where she won all the chips at the table she would have $1,000 right now, but it is a tournament so her winnings are capped.
Where has the other $500 in equity gone? It has gone to the runner-up and third place finisher in the form of payouts.
This difference between tournaments and cash games has major strategic implications. If you make a $100 bet in a cash game and get called, you win $200 when you have the best hand. This 1:1 ratio is what is called a Chip EV (cEV) situation. If you bet your 100 chips in our example tournament you risk $100 of equity, but you do not get $100 in real money equity back when you win. It varies, but you always stand to win less than you risk in any tournament decision (except in PKO tournaments). The broad strategic adjustment is to, therefore, play tighter in tournaments than you would in cash games.
Consider the following example, which you can replicate yourself using the free ICM calculator at ICMIZER.com. It’s the start of that rakeless $100 tournament with 10 players and $500/$300/$200 payouts. Let’s say that two players go all-in against each other, blind vs blind, and one player is eliminated, meaning that nine players remain, one has 200 chips and the other eight still have their 100 chip starting stack.
What would you say the equity was of the new chip leader?
If you said $200, you would be wrong. If this was a cash game that would be correct, but the actual answer is $184.44.
Where did the other $15.56 go?
It went to the other eight players.
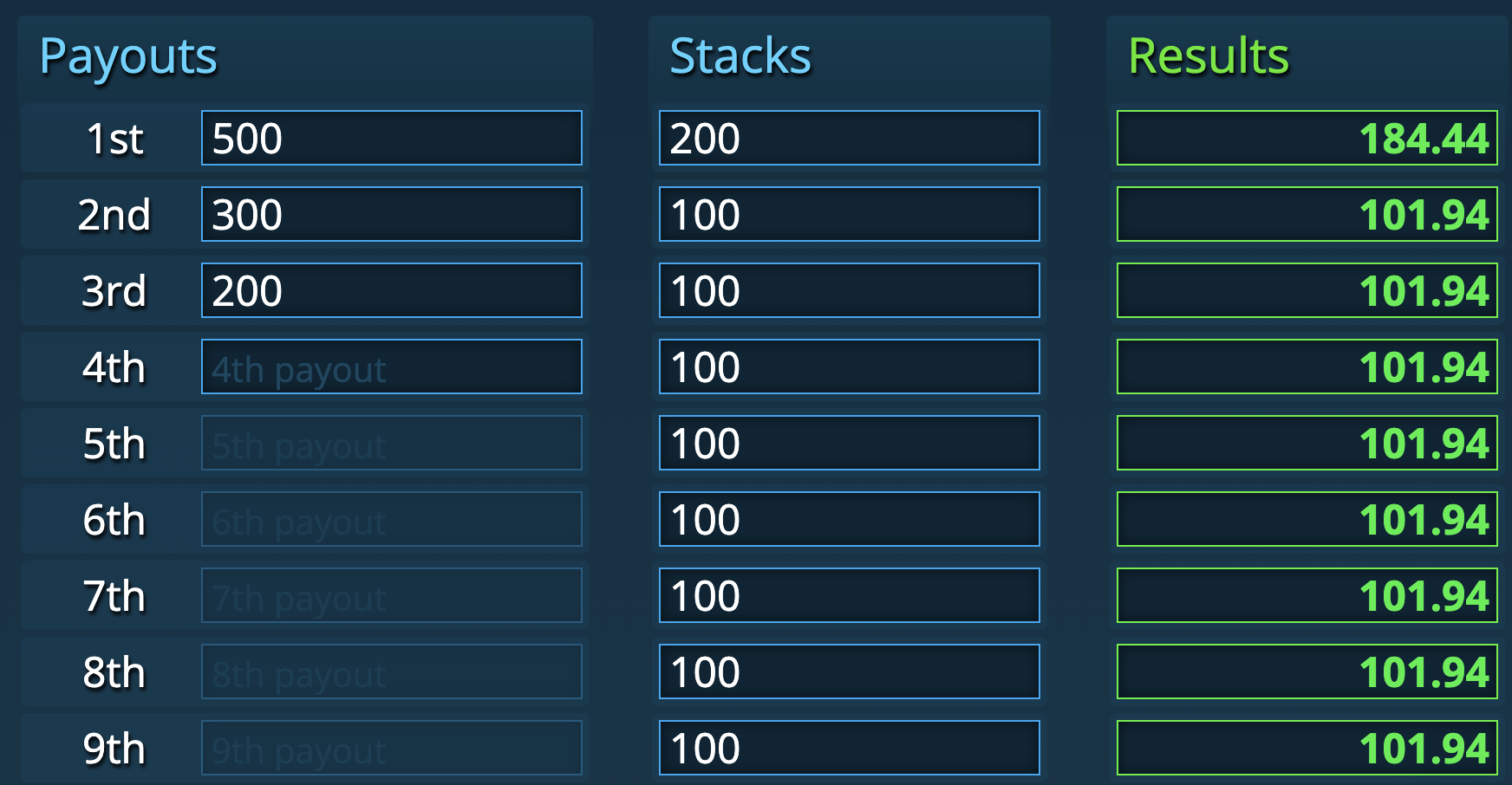
The other players gained $1.94 in equity each without having to risk a single chip. By eliminating another player, the chip leader essentially improved everyone else’s equity by moving them one step closer to the money.
The chip leader risked $100 in equity (their whole buy-in) but only gained $84.44. This is a constant in tournaments, you always risk more equity than you stand to gain, even though there is a 1:1 ratio in chips.
If this was a cash game and you risked $100 to win $100, you would only need 50% equity to break even. However, in this example if you risk $100 to win $84.44, which means you need 54% equity for this to be break even.
This example also highlights something else that makes tournaments unique, which is that folding can be profitable. In this example everyone at the table made $1.94 in equity by sitting on their hands and doing nothing. If this was a final table they would literally move up one stage in the payouts just for folding, which is known as laddering.
Understanding ICM poker means you will often adopt the mantra in poker that tight is right in tournaments.
How ICM works
To do an ICM calculation you only need two pieces of information – the chip stacks and the payouts. Position, the blinds and antes, the clock, the skill of the players – none of these matter.
An ICM calculation is essentially a very complicated calculation of the odds of every possible combination of finishing position amongst the players. It starts of very simple, the odds of each player coming 1st is literally their percentage of all the chips in play. So in the example above the chip leader (who we will call Player 1) is a 20% favourite to win, everyone else has a 10% chance.
After that it gets complicated because you have to work out what the chances are of Player 2 coming 2nd if Player 1 comes first, the chances of Player 1 coming 2nd if Player 2 comes first, the chances of Player 2 coming 2nd if Player 3 comes first, and so on. Below is an example of what the actual finish distributions would be in our example. Don’t pay more than a glancing look at it, it is incredibly complicated and requires a powerful computer to work out.
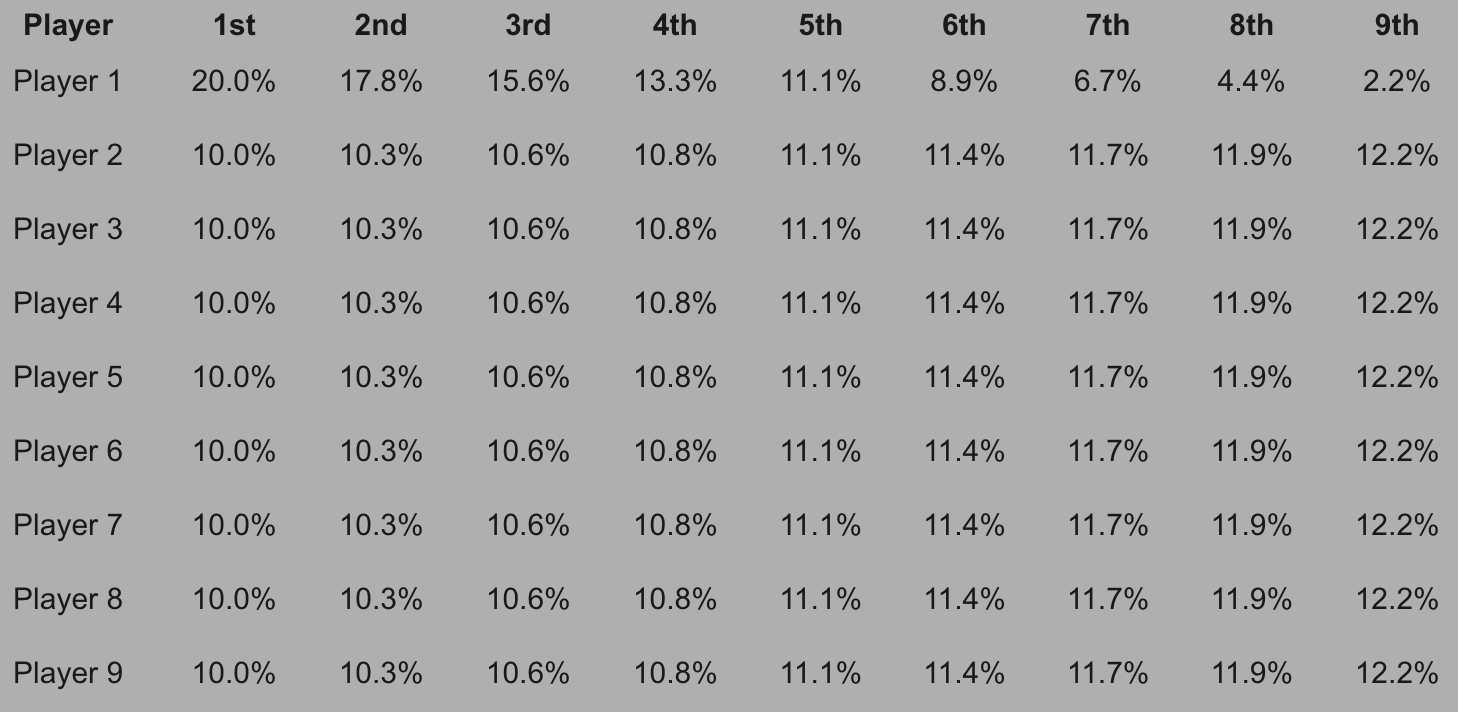
Thankfully there are calculations, heuristics and solvers like ICMIZER available that simplify understanding ICM poker so that you do not need to memorise things like the above example. When you use a tool like ICMIZER you an extrapolate broad takeaways about ICM that you can take to the tables and enjoy a big edge over your opponents.
Now we have shown you what goes into an ICM calculation, let’s look at an example of how strategy changes when ICM is a factor. We are five handed in an SNG with 500/300/200 payouts like above, so we are two away from the money. In this example three players have folded and the chip leader has gone all-in with 30 big blinds against the Big Blind who has 11 big blinds. If they lose this hand they are out of the tournament so close to the money.

First of all let’s look at what ICMIZER says they should do if this were NOT a tournament, ie. A ChipEV spot:
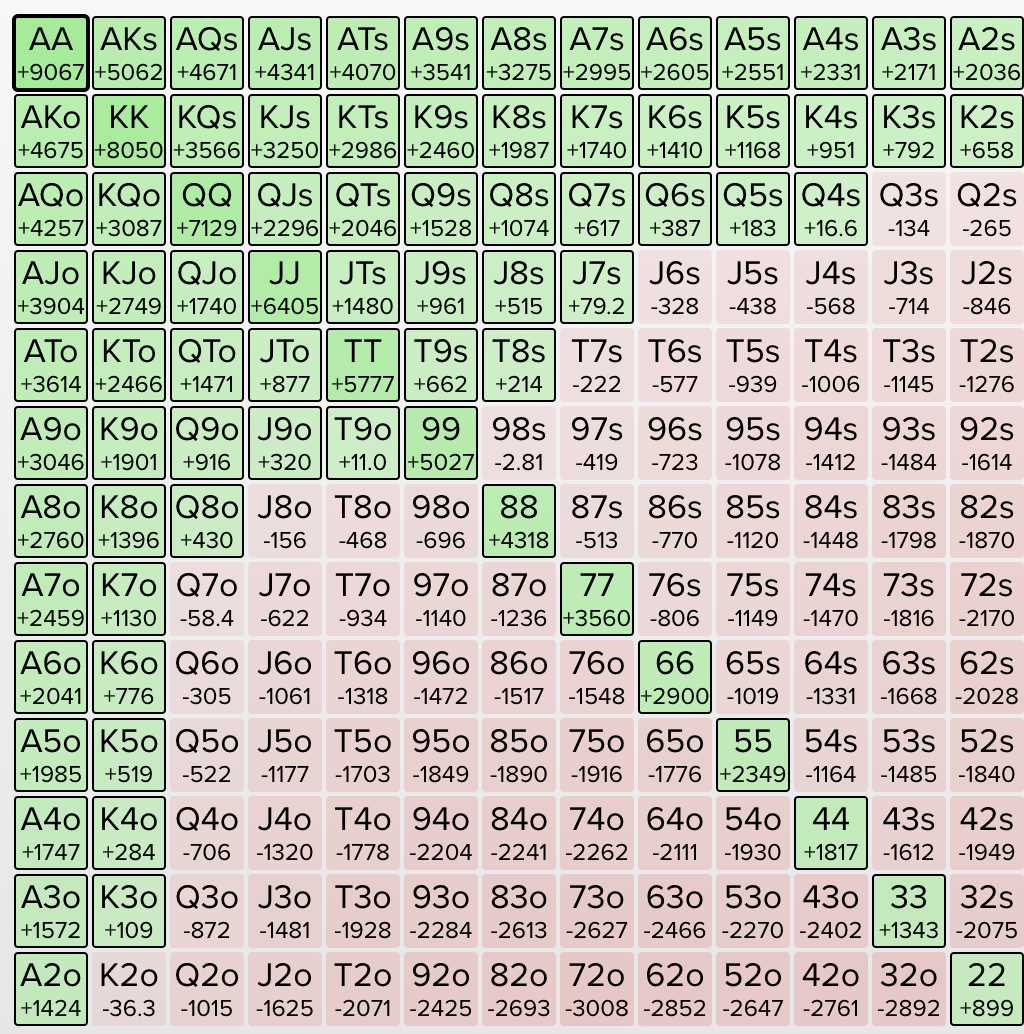
This is the range of hands the Big Blind can call with profitably. As you can see it is the top 43% of hands. The Small Blind is expected to be shoving a wide range here so the Big Blind can also call with a very wide range.
Let’s look at the exact same situation, but now in a tournament with ICM a factor and two players left before the money. This is the new Big Blind calling range:
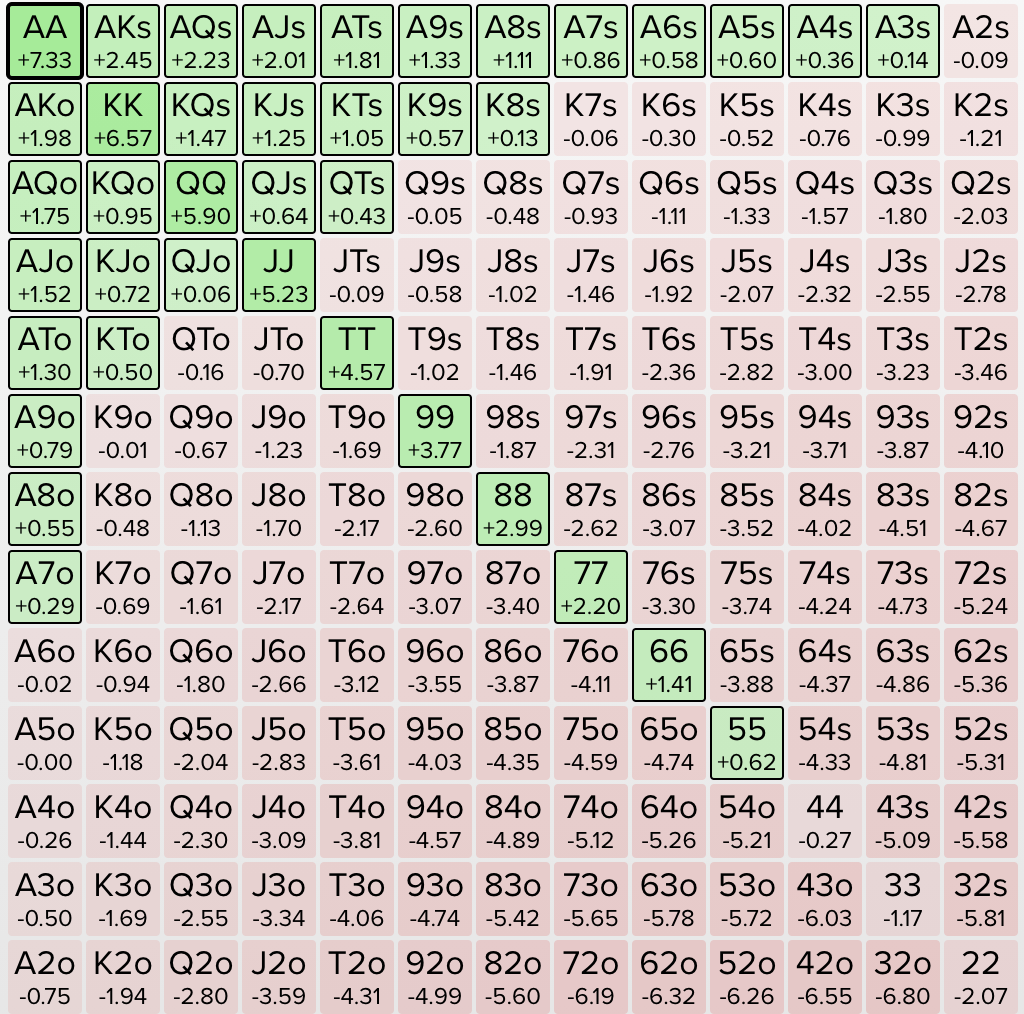
It has more than halved from the top 43% of hands to just the top 20%. You need a much stronger hand to risk elimination in a tournament because the equity you gain when you win is always less than the equity you risk. For this reason, the Small Blind can shove more hands, in the first example they shoved the top 63% of hands, in this example they can profitably shove 100% of their hands, because the Big Blind has to fold more often.
You will also notice that the shape of the range changes slightly too, it doesn’t decrease from 43% to 20% in a linear fashion. Offsuit Ax/Kx hands and small pairs are removed from the range before suited Ax/Kx hands. In a vacuum 22 and A2o are stronger hands than K8s, but K8s is profitable because it blocks some of the strongest hands, makes good top pairs and has good equity against strong hands. 22 is always in at least a coinflip, which you want to avoid when ICM is a factor. You cannot just tighten your range with ICM, you need to change the types of hands you play, which a tool like ICMIZER can show you how to do.
This is a very simple example that highlights the biggest strategic adjustment where ICM is concerned. If you are at risk you should play very tight because the downside of losing is far greater than the upside of winning. If, however, you have a big stack you can play much more aggressively because your opponents should be folding more.
When does ICM factor in tournaments?
It is a common myth that ICM only factors on the bubble of tournaments and at final tables. Nothing could be further from the truth. As you have seen from the example at the start when two players go all-in on the first hand of the tournament, ICM plays a role from the first hand. Very few players realise this and adjust accordingly, many play a ChipEV strategy until the bubble is looming, which is a mistake.
ICM gets more severe the closer you are to the money and is at its most extreme on the bubble. It then drops down significantly after the bubble bursts but creeps back up as the final table bubble approaches.
Contrary to popular opinion, ICM gets less extreme with each elimination at the final table. Players assume ICM is more extreme three handed than nine handed because the payouts are larger. The truth is ICM is less extreme because the remaining players have locked up more money and the remaining amount of equity they are playing for is less, relatively speaking.
There is no ICM heads-up, it is the only stage of a tournament where that is the case. A tournament needs at least two payouts for it to have ICM in it, which is not the case heads-up. You have both locked up 2nd place prize money and are now playing for the difference between 2nd and 1st.
This illustration of ‘Bubble Factor’ in the Sunday Million charts how extreme ICM is at different stages of the tournament. Bubble Factor is a useful guide that shows you how tight or loose you can play, relatively, against other players at the table. Bubble Factor is also displayed on every ICMIZER calculation. Below shows the average Bubble Factor of the average player in the tournament:
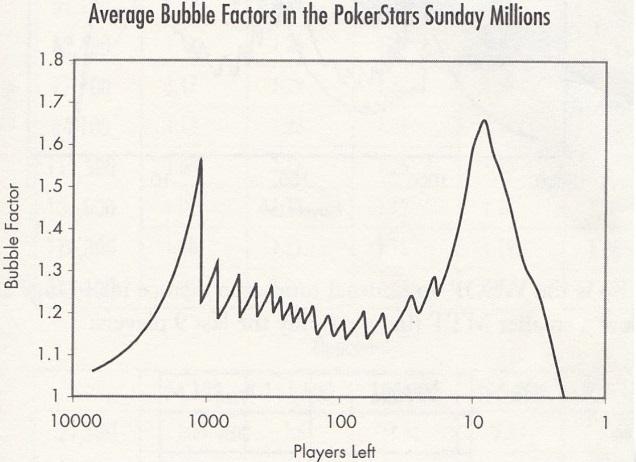
ICM is more extreme in some formats than others. There is no ICM in Winner-Take-All MTTs and standard Spin & Gos, those are essentially cash games with increasing blinds. Satellites and Double or Nothings have the most extreme ICM, because all the prizes are of equal value, so there is no benefit for having the most chips. There are actually spots in satellites where folding Pocket Aces is correct, because the downside of losing is so severe.
Formats with ‘flat’ payout structures (ie. Where the difference between the top prizes is less than usual) are more ICM extreme. Tournaments with top heavy first prizes have less ICM because there is more impetus to try and ‘play for the win’. PKO and bounty tournaments have less ICM in them because you have more incentive to play loose to win bounties. In fact there are many spots in PKOs where ICM flips on its head and you can call wider than cEV when a big bounty is on the table.
ICM and final table deals
Most people have their first introduction to ICM when they make a final table and are offered a deal. The deal that is usually proposed is an ICM deal, in other words everyone is offered a money amount based on what their stack is currently worth. Making a final table is a relatively rare thing, especially in big MTTs, and most of them end in deals because the players like to avoid variance.
This is an example of a final table deal which you can replicate yourself using the free tool at ICMIZER.com.
Five players remain in a $10 MTT with the following chip stacks and payouts:
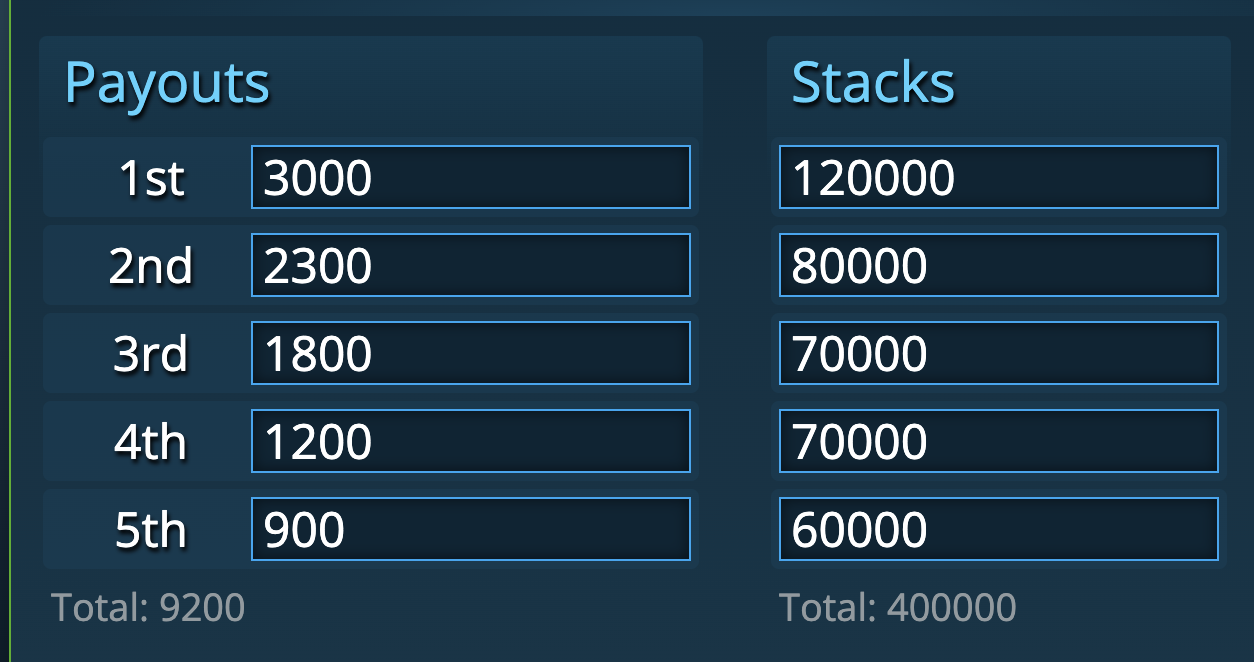
The top prize is $3,000 which is a very nice payday for a $10 tournament and everyone has $900 locked up. The chip leader has 30% of the chips in play and double that of the shortest stack.
Before going any further, look at the stacks and payouts. What do you think each stack is worth if the players dealt right now? What would you want to guarantee as the chipleader and what would make you happy to end the MTT now as the short stack?
This is what the actual values of each stack are:
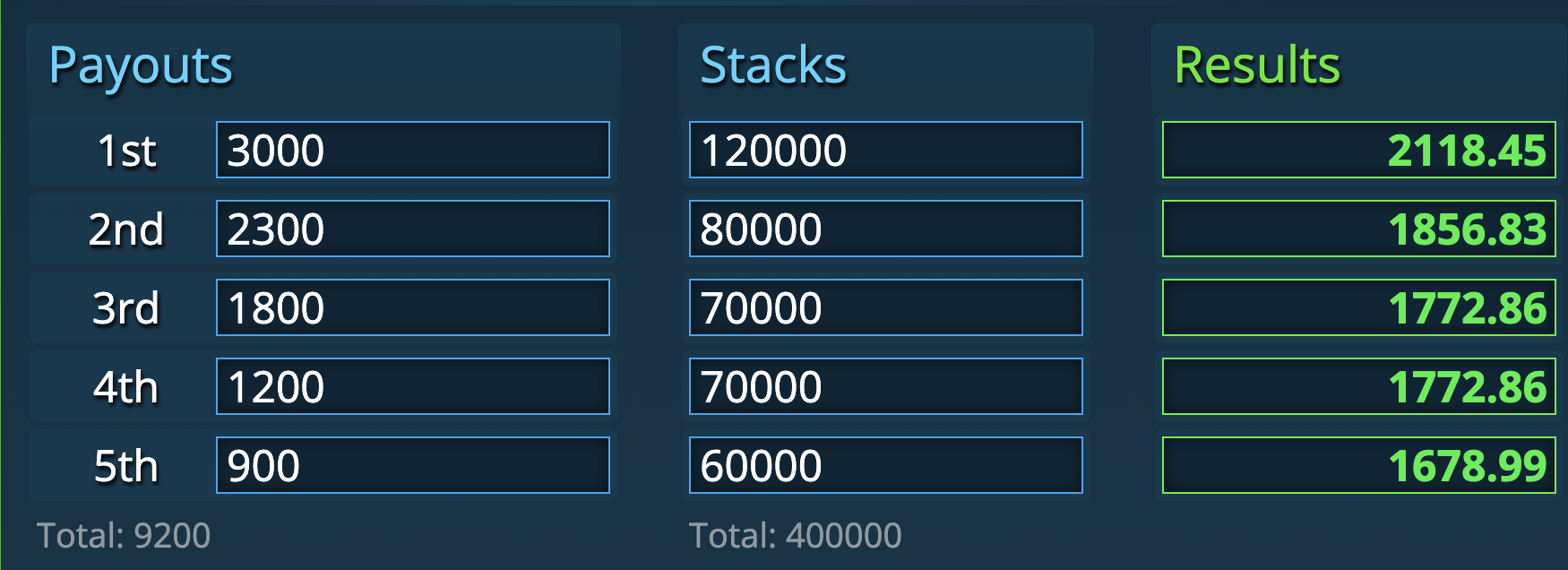
Players are often surprised at how little the chip leader is worth and how much the short stack should deal for. Even though the leader has twice the chips of the short stack, there is only $439.46 difference between the two, which is less than a quarter of what the big stack is worth.
This goes back to what we discussed about there always being more downswide than upside in tournament decisions. The chipleader’s winnings are capped, no matter how many chips they have they can never win more than $3,000 here. The short stack, however, has more upside relatively. They are currently guaranteed $900 and their equity is $1,678.99 – it is often going to be in their interest to play on because they can win much more.
If you are looking at the chipleader’s equity and wondering why they would ever deal, the answer is to avoid variance. A couple of unlucky hands in a row and the chipleader could easily be the next player out, wishing they had dealt. Final tables are rare and dealing for $2,118.45 might provide that player with a big enough bankroll boost to move up the stakes. It might be the case that this is the biggest final table this player will make this year and it might be the thing that determines how good a year that player had. The difference between $3k and $2k might not be much, they are both great results, but having to settle for $900 might be a disaster.
These are the ICM finish positions for each player:
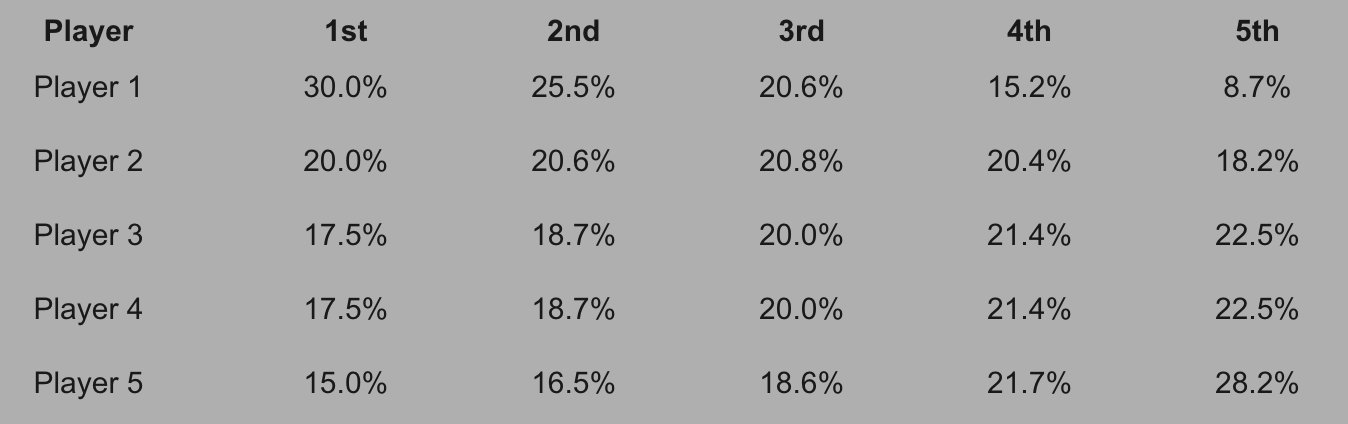
The chipleader wins 30% of the time, but they take down an amount less than the deal being offered 54.5% of the time. More often than not, they would have been better off taking the deal. The short stack finishes in 5th place 28.2% of the time, but they win a prize bigger than the 4th place prize 50.1% of the time. This is why they get a favourable ICM offer, because half the time they should expect to come third or better.
As we have previously mentioned, ICM does not account for skill. It is likely the case that a good professional at this table might win the tournament more than the above figures would suggest. A top online crusher with the chip lead might win this 35% of the time, for example. This is why some top players should reject ICM deals. You might see a serious player with the chip lead ask for something like $2,400 in the above example. If the rest of the table agree, they would divide the remaining prize pool up by the same proportions as the previous deal.
There is also the human psychology side to deals. A bad player who is already very rich outside of poker might be able to negotiate a better-than-ICM deal because the money doesn’t mean as much to them as it does the rest of the table. Some players might have a specific amount in mind because it would buy them something they want, or get them out of debt, or allow them to move up in stakes. These players will often be unwilling to deal for less than the amount they have in their head, even if the deal is a good one.
The ’correct’ amount to deal for is whatever amount you would be happy with, so don’t allow yourself to get pressured into a bad one. However, always look at ICM as the starting point for making any deal.
The limitations of ICM
All the top professionals use ICM and you should too, but it is by no means perfect and you need to know where it falls short.
First of all, it does not account for skill, it assumes all players are of equal ability. If you are, for example, a professional player then you might not want to accept an ICM final table deal because, on average, you should expect to win more than that. ICM might say you win 20% of the time but with your edge you might win 25% of the time. This also factors in to your decisions at the table. If you have a big skill edge then you should avoid high variance spots with the bottom of your range and potentially play even tighter than ICM dictates. In the example hand example from earlier K8s is barely profitable, if you are a skilled player you might want to fold a hand like that because you can expect to make more money, on average, by avoiding elimination and staying in the game. In contrast if you are an underdog at the table you should not pass up any profitable spots, however marginal.
ICM does not account for future game. That is, it does not factor in what your next decisions might be when this hand ends. ICM actually assumes the game ends now, which most of the time it obviously does not. After you decide to call/shove/fold you will have a new chip stack the next hand and a new decision to make, which ICM does not factor in.
ICM simply gives us a model to estimate the value of a stack of chips, and then we use those estimated values to compare the different plays we can choose from by modeling a real hand of poker, accounting for blinds and skill (ranges chosen) for that one hand. But at the end of that model for that one hand, once again, ICM assumes that everything stops and all players are immediately paid their ICM equity of the prize pool and all of the information that exists in the real world (skill, rotating and increasing blinds, etc) is ignored.
Let’s take a look at a hand example, an extreme yet common case on the bubble of a 6max SNG - where the SB is considering a shove into the chip-leading BB, while the short stack button player has only one blind left - to see how a single poker hand modeled with ICM suffers from the ignorance of rotating blinds.
Tournament: 6max SnG
Payouts: 1st - $65, 2nd - $35
Blinds: 100/200
BTN: 200, SB: 400, BB: 2,400
Preflop: Action to Hero on the Button
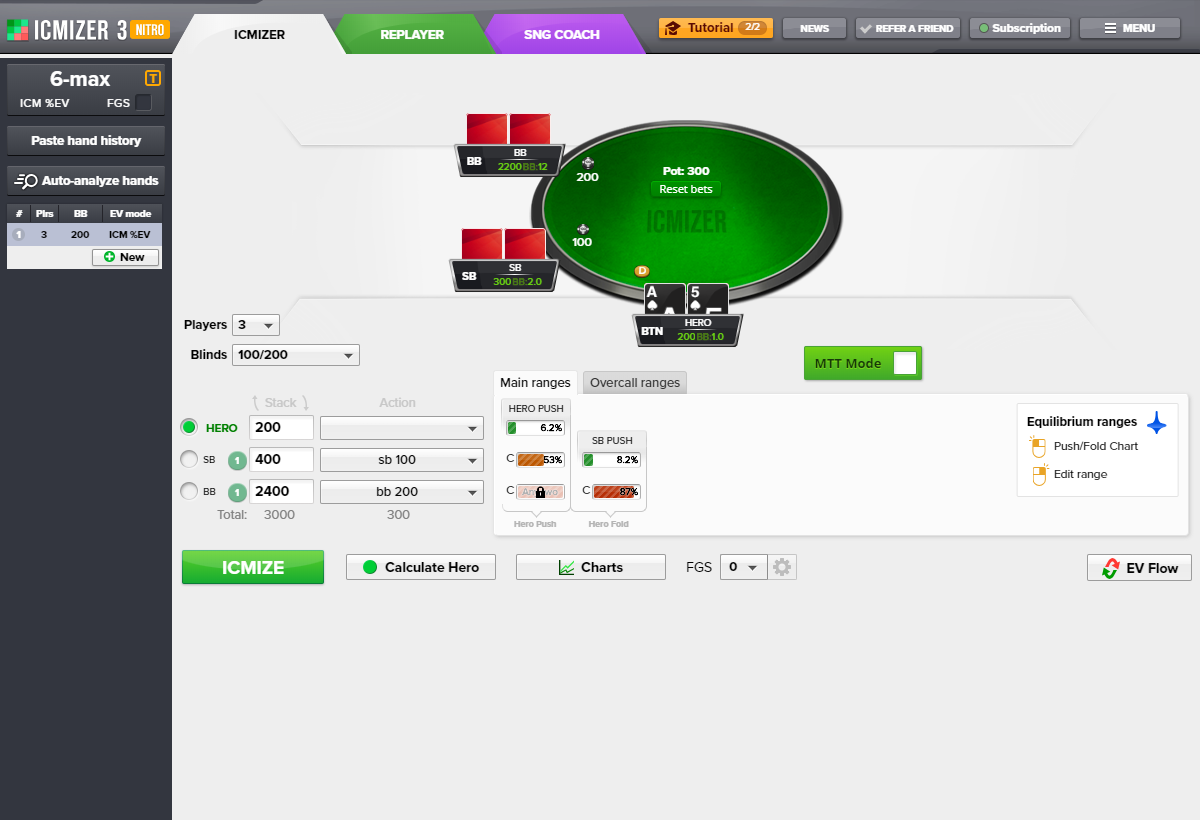
To speed things up we won’t be doing any work by hand here, we’ll just look at the results of an ICMIZER calculation and assume a Nash Equilibrium calling range for the big blind.
At equilibrium in this push/fold game modeled with ICM, the BTN should be pushing just 6.2% hands and SB who is medium stack should shove roughly 10% of the time. Certainly there is merit to the BTN folding some hands—there is a chance that if he folds SB and BB will go all-in against each other and that would be a great outcome for the button player. However, ICM suggests only 6.2% push which may sound strange to a player with some poker intuiton, so we need to think about what ICM takes into account and what it actually ignores here. It becomes immediately apparent that there is a big flaw that requires an obvious adjustment.
ICM assumes that, at the end of the hand, all things are equal and everyone gets paid their ICM equity share of the prize pool. So in this example it assumes that the BTN is going to get paid at the end of this hand based on his 200 chip stack.
But all things aren’t equal, and we know that in the next hand that BTN short stack will have to post his blind all-in with any hand he is dealt, clearly this event is much worse for the short stack than the naive assumption that he’ll be awarded his equity next hand - and that loss for the short stack is a gain for the others. This issue is always present with ICM calculations, although at deeper stacks and further away from the bubble it’s effects are lessened.
This is where FGS model with varying depth comes to the rescue. If we calculate the optimal ranges in the same situations with the FGS of depth 5 (which means that ICMIZER will be looking 5 hands ahead), we can see a very different pushing range for SB player and calling range for BB player:
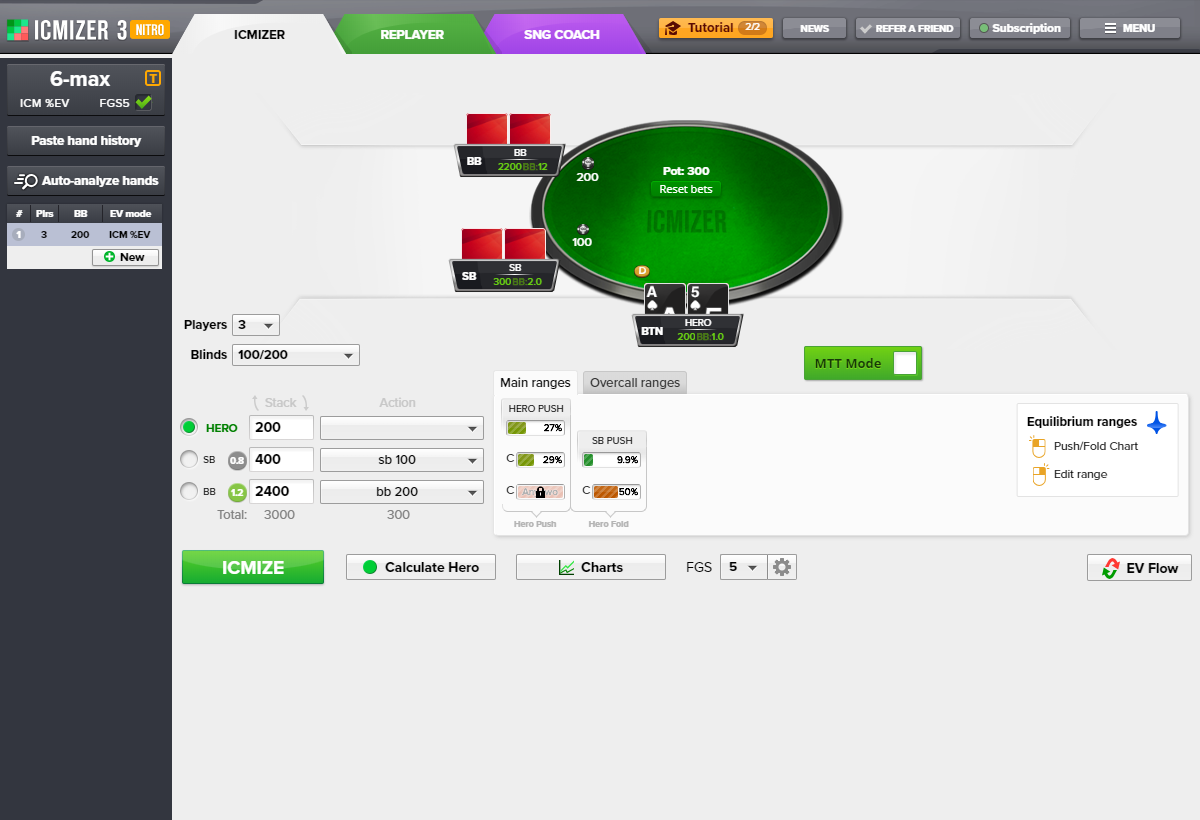
We can see that the pushing range has increased significantly, now to 27% percent which represents the following hands: 44+,A2s+,A3o+,K6s+,K9o+,Q9s+,QTo+,JTs. It also makes much more sense intuitively.
There have been successful attempts to improve ICM’s accuracy by addressing the flaws we mentioned here. The model that is currently trusted by poker professionals is Future Game Simulation (FGS) which uses ICM at it’s core and takes the method we used in this article of modeling a poker hand a step (or several steps) deeper by modeling a number of hands which will follow the current one. This model effectively accounts for issues like order of posting the blinds or short stacks at the table.
With ICMIZER you can review any tournament hand with ease. The most powerful software & mathematical tools are at your disposal: FGS & ICM models, Nash equilibrium approximations and precise equity calculations guarantee powerful strategies and minimize the amount of mistakes that you will make at the table.
How to develop your ICM skill
Most people realise they need to know more about ICM after they make a big final table. If they played on and made a big ICM error, or they accepted a worse than ICM deal, it could have a profound negative impact on the trajectory of their career. As a tournament player the most costly errors you will make are ICM mistakes. So how can we improve our ICM poker skills so that we do not make huge ‘ICM punts’ when the pressure is on?
ICMIZER is an advanced endgame analysis tool that can solve any preflop ICM spot in poker. Whether it is SNGS, MTTs, satellites, PKOs or even ChipEV spots, if you input the stacks, prizes and positions, ICMIZER will provide you with the Game Theory Optimal (GTO) shove and call ranges for every player at the table. If you had a tough spot at a final table, ICMIZER can review it for you.
You can also adjust your opponent’s ranges, because the chances are that they will not be playing GTO ranges. Some players will be playing too loose, some will be playing too tight and others will be playing the wrong types of hands. ICMIZER will show you how to play against typical real life opponents, although the outputs are only as good as your assumptions about how your opponent’s play.
If you really want to understand ICM it is particularly useful to simulate the same hand twice in ICMIZER. First as ChipEV and then again using the actual tournament payouts. You will notice that both the shove and call ranges differ greatly in the two situations. Not only are the calling ranges typically tighter (and sometimes as a result the shoving ranges wider) but the types of hands you play differ. You are more likely to see a greater concentration of Ace high hands and less small pairs/suited connectors in an ICM range, because they ‘block’ the typically tighter ranges your opponents would be playing.
The most valuable aspect of ICMIZER is the MTT Coach feature. This is a training tool that puts you in realistic push/fold spots in all manner of poker formats and quizzes you about the correct hands that should be in your range. You can go as broad or as detailed as you like. You can train yourself on MTT spots in general or get really specific, for example short stack spots with four players left in a 9-man SNG.
It is very expensive to make a big ICM mistake at the tables, but you can simulate thousands upon thousands of these spots every day in ICMIZER. It is precisely the tool you need to train your muscle memory so that the right decisions come automatically at the tables. There is even a leaderboard feature so that you have something to motivate you to train your hardest.