Ben Roberts ICM model
by Q.
In this article Ben Roberts gives an introduction and reasoning behind his/her new ICM model. He compares new algorithm with classic Malmuth-Harville ICM algorithm.
Introduction of new ICM model
For many years, poker players have estimated tournament equity using the
Independent Chip Model (ICM). This model is based upon the assumption that
a tournament evolves by repeatedly choosing two random players and moving
a chip from one to the other. The motivation behind the ICM assumption is
to de ne players' equities independently of blind/ante structure, position, and
player skill. This ignorance of realistic factors is a common criticism of the ICM,
however (as far as I know) no viable alternative model has been implemented
that does account for such complications.
Despite the simplicities created by the ICM assumption, actually calculating
the subsequent equities is still a challenging task, with standard procedure being
to use the Malmuth-Harville (MH) algorithm to estimate them. This is where
my new algorithm presents an advance over current practices, as the estimates
produced have without exception proven to be significantly more accurate than
the MH algorithm. To be clear, my algorithm is better at estimating equities
under the ICM assumption. It is not clear whether or not it produces more
realistic results, as it still contains the weaknesses inherent in the ICM model.
To summarize, the calculation of ICM equity introduces essentially two
sources of error: the error created by ignoring realistic factors, and the error created by inaccuracies in the estimation procedure. My algorithm doesn't
address the first type of error, but significantly reduces the second type. Addressing the question of whether or not it produces more realistic results, the
optimal calling/shoving ranges found using my algorithm are more consistent
with my intuition, however I'm not a tournament player so it would be interesting to get the opinion of experienced SnG and MTT players.
Examples of applying different ICM models to same situations
In general, the MH algorithm tends to overvalue short stacks and undervalue
large stacks. My algorithm (which for lack of a better name let's call the Ben
Roberts (BR) algorithm) rectifies this discrepancy as one can see from Table 1.1
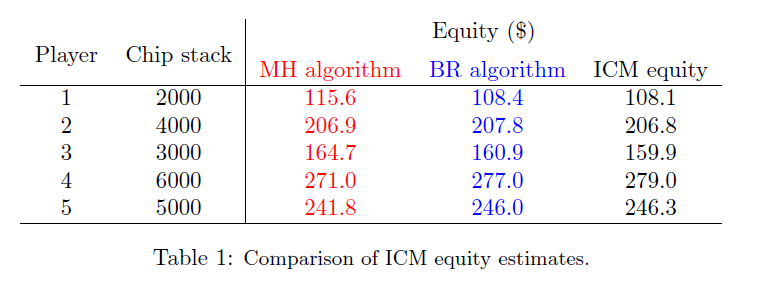
Note: Accurate ICM equities in the third column of Table 1 were calculated through Monte
Carlo simulation with 1 000 000 samples. In each sample, blocks of 1000 chips were iteratively
moved from a random player to another until enough eliminations occurred. The ICM equities
turn out to be pretty robust when it comes to the size of the blocks getting moved around,
provided each chip stack is some whole multiple of the block size.
As a result, the MH algorithm is more apt to preserving short stacks and
gambling with large stacks, which we can see from the ICMIZER simulations in
Figures 1 and 2. That is, assuming 3-handed bubble play in a 6-handed SnG
that pays 65%/35% and blinds of 50/100:
- If a big stack with 1500 chips blind shoves from BTN, SB with 1000 chips
folds, and we're in the BB with 500 chips, the MH algorithm advocates an
optimal calling range of 57.8% while the BR algorithm advocates 72.5%.
- If a short stack with 500 chips blind shoves from BTN, SB with 1000 chips
folds, and we're in the BB with 1500 chips, the MH algorithm advocates
calling 78.9% while the BR algorithm advocates 69.5%.
The results from the BR algorithm make more sense to me, as I can't understand
trying so hard to preserve a short stack that very likely needs to gamble soon
anyway. In contrast, there seems to me more value in preserving a large stack
that can put pressure on one's opponents. Therefore, these simulations suggest
(according to my intuition anyway) that the BR algorithm is not only more
accurate with respect to the ICM model but also more reflective of real equities.
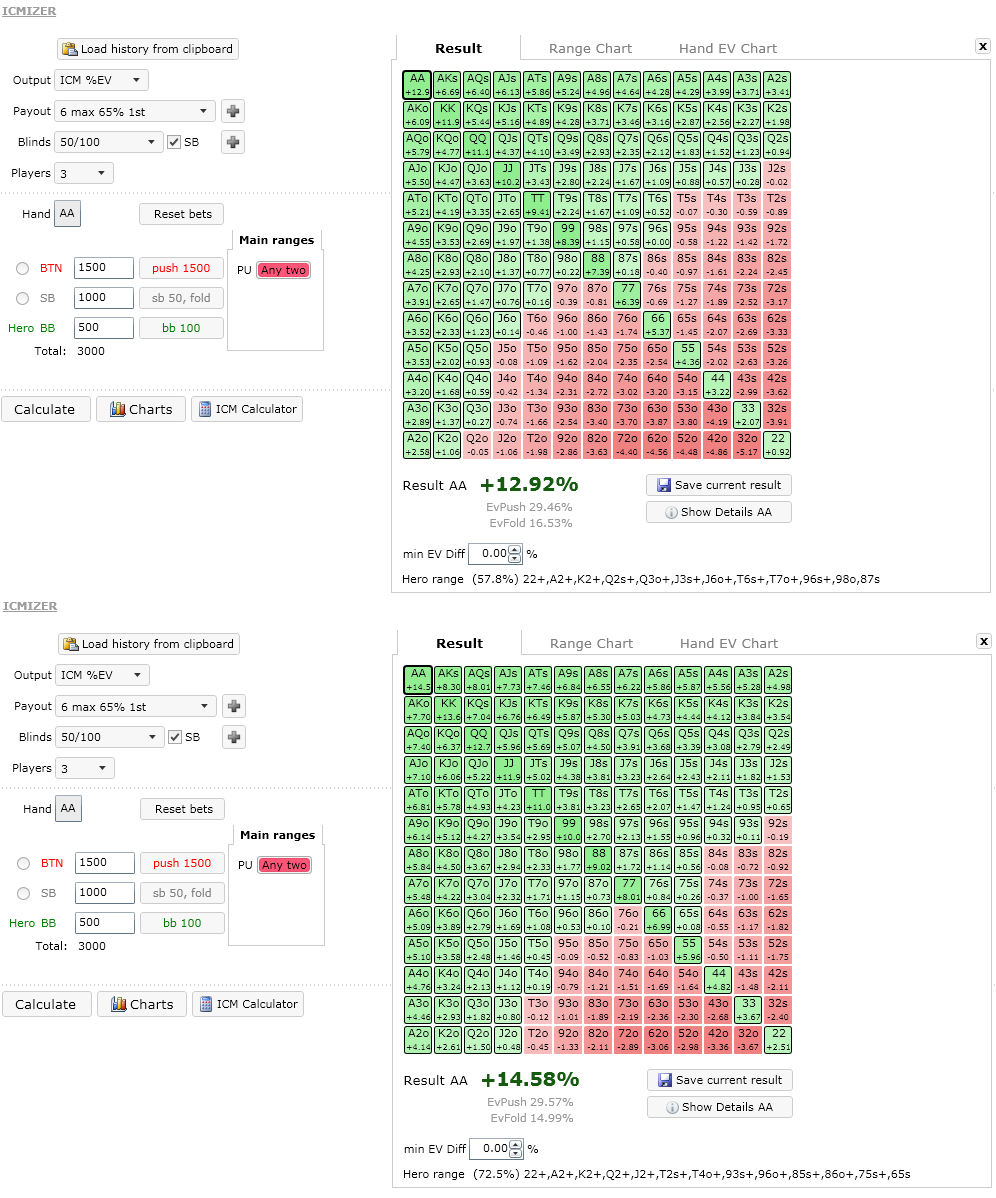
Figure 1. Bubble calling as short stack versus big stack calculated with different ICM models
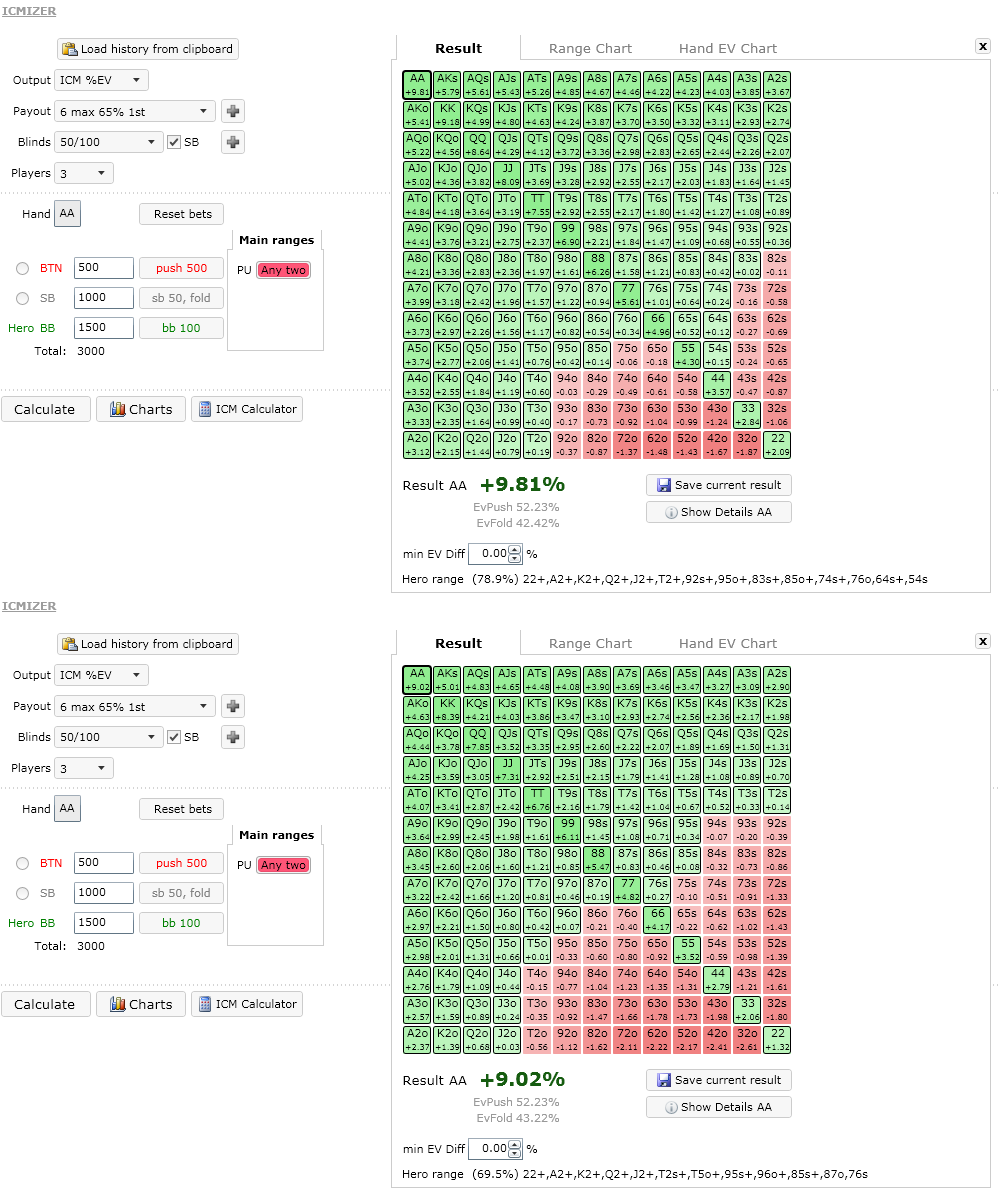
Figure 2. Bubble calling as big stack versus short stack calculated with different ICM models
Article by Ben Roberts, March 11 2012
Please leave any questions in comments