In my last post I looked at short stacked shoving tactics on the bubble. In this post, I would like to focus on short stacked all-in call ranges when in the bubble period. It seems regs these days know how to play the big stack and mid-stack very well on the bubble. Correctly, many regs know to be ruthless with the big stack and push the other stacks around and to play a conservative game as the mid-stack when facing resistance from the big stack.
However, one stack many people misplay on the bubble in my experience is the short stack. Time and time again, I see players call off far too wide against the big stack, particularly when even short stacked with another opponent on the bubble. Indeed, it is true that when clear short stacked on the bubble you have the least to lose so can afford to take more risks, especially in contrast to the mid-stack who has to adopt a much more cautious approach. However, it seems that some players once short stacked denote 0 value to their stack and completely abandon ICM priority: colliding with the mid-stack or the other short stack whose chips are worth a lot more money.
Understanding this further, I thought I would demonstrate the above by looking at a couple of examples in ICMIZER before offering a more in-depth explanation:
Bubble scenario 1: big stack and short stacks with 20% of his chips
So I've created a typical 6max bubble situation in ICMIZER with the big stack open-jamming from the BTN and assigned both of the blinds identical stacks and situated the hero in the SB. To get an idea of how wide we can call off against the big stack, I've assigned the BTN the Nash equilibrium range which in this spot is 97% of cards. This assumes that both of the blinds are calling correctly; if either opponent were to call particularly loose then pushing the Nash range will be incorrect on behalf of the big stack. One benefit of looking at it from this point of view is if it's incorrect to call off with a particular hand then you know it can't ever be correct regardless of their range, so that should help you out in future situations with similar dynamics. I've assigned the BB in this instance a respectable overcall range of 3.5% (10s+/AKs/AKo) and a call range of 7.54% against the big stack if we fold, so this also assumes he's a capable player. This will avoid any obvious biased results in the calculation i.e. if the BBs range for calling off the big stack was very wide then it will be incorrect for the hero to call off with some quality hands that may normally be a call.
http://www.icmpoker.com/icmizer/#Aafu
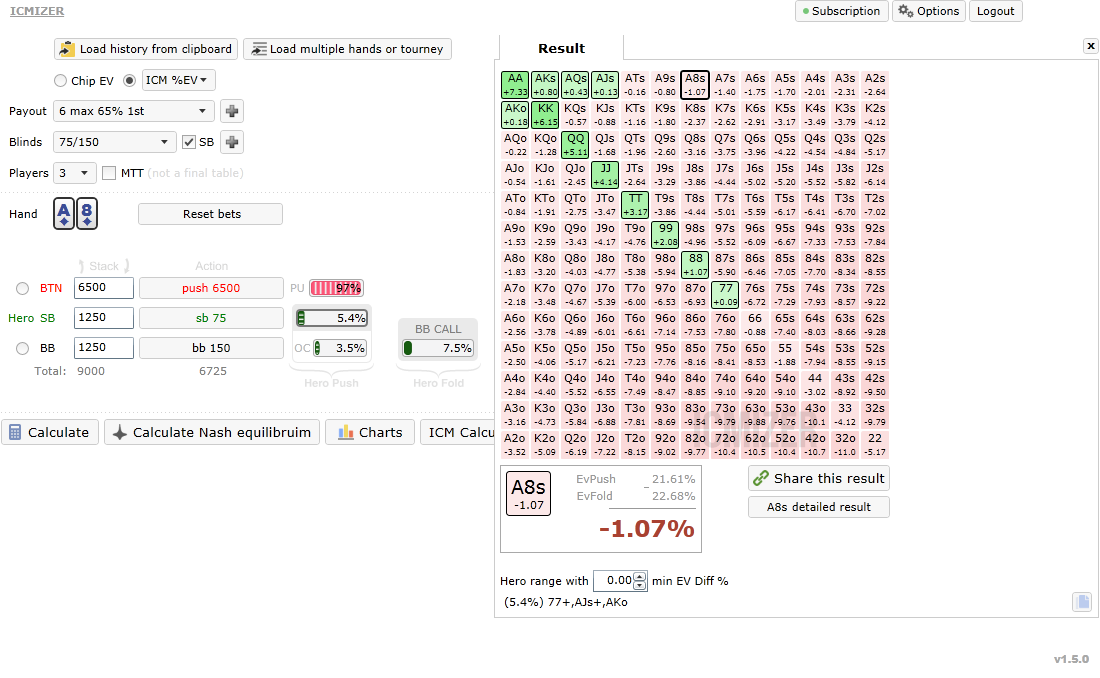
The result
And what do you know...
We can only call off with 5% in this spot and it loses money to call off with AQo. It's not uncommon to see players snap call with A-Qo and even much wider and to do so is simply throwing your money away. Calling off with A-8 suited for instance costs more than 1% of the prize pool which is pretty criminal but something you’ll observe fairly often. And remember, this is against a big stack who knows ICM and elects to shove almost any two cards here; if you were up against a tight BTN or a player who didn't know ICM and the power of their big stack then they would be pushing way tighter than this range which in turn means the hero's range for calling off would be tighter.
So, the question remains: Why do we call so tight against the super wide big stack here only 8.33bbs deep?
ICM
First and foremost, the most predominant factor here is ICM. In a 6max SNG, the top two finishes are paid. This means that the short stack's chips are worth a lot more money to us than the big stack's since if we collide with the short stack and prevail we'll instantly have at least 35% equity locked up (what 2nd place pays) giving that the stacks are identical in this situation. However, if we collide with the big stack, the bubble continues even if we win so we can never immediately make money here and only instantly lose money by being all-in in this situation. To support this, let's take a look at what happens to the equity of our stack the times we collide with the short stack and then the big stack.
Equity of the stacks
Equity of the stacks
Big stack: 55.10%, Hero: 22.45%, BB: 22.45%
It should be obvious our equity is identical to the BB given that the stacks are identical. Now, let's say we collide with the other short stack and win, the equities are now:
Big stack: 56.67%, Hero: 43.33%, BB: 0% (busted)
So, if we collide with the short stack and bust him, our equity increases from 22.45% to 43.33% - so our equity almost doubles, and we have 35% of the pool secure (2nd place). Remember, by doubling up in chips in a tournament your equity will never exactly double since the more chips you have the less value they become worth – this is because of ICM i.e. the fact you can end up with all the chips at the end of a tournament but only win a certain portion of the prize pool.
Now, let's see what happens to the numbers if we collide with the big stack and win:
Big stack: 49.06%, Hero: 33.23%, BB: 17.7%
Our equity only increases by ~11% from 22.45% to 33.23%!
Obviously if we lose the all-in in either case our equity drops to 0% since we'll bust giving that both the short stacks are identical but you can see that the equity increase of our stack is much greater when colliding with the other short stack and this is simply a result of the stack sizes in relation to the pay-out structure or what otherwise is known as ICM.
Future $EV
ICM calculators although great for telling us the immediate EV of a move fail to account for the bigger picture i.e. what may happen in the following 10+ hands of the tournament. With this in mind, it's worth thinking about what is likely to happen if we double up against the big stack here. We will become a clear mid-stack on the bubble so our opponent if any clue about ICM will raise and shove wider into us and with more equity to protect our all-in call ranges will tighten up. This basically means we’ll have very poor future EV. This of course assumes the big stack knows how to play the big stack but either way, there isn't any significant advantage to doubling up, especially since we won't have a lot of chips and won't be in the position to do any serious damage.
However, there may be some merit to doubling up if we had more chips and were gaining more of the prize pool. So, let's take a look at a comparable situation but this time stripping away some of the big stack's chips and assigning both the short stack's 2k in chips:
Bubble scenario 2: big stack and short stacks with 40% of his chips
http://www.icmpoker.com/icmizer/#uPKZ
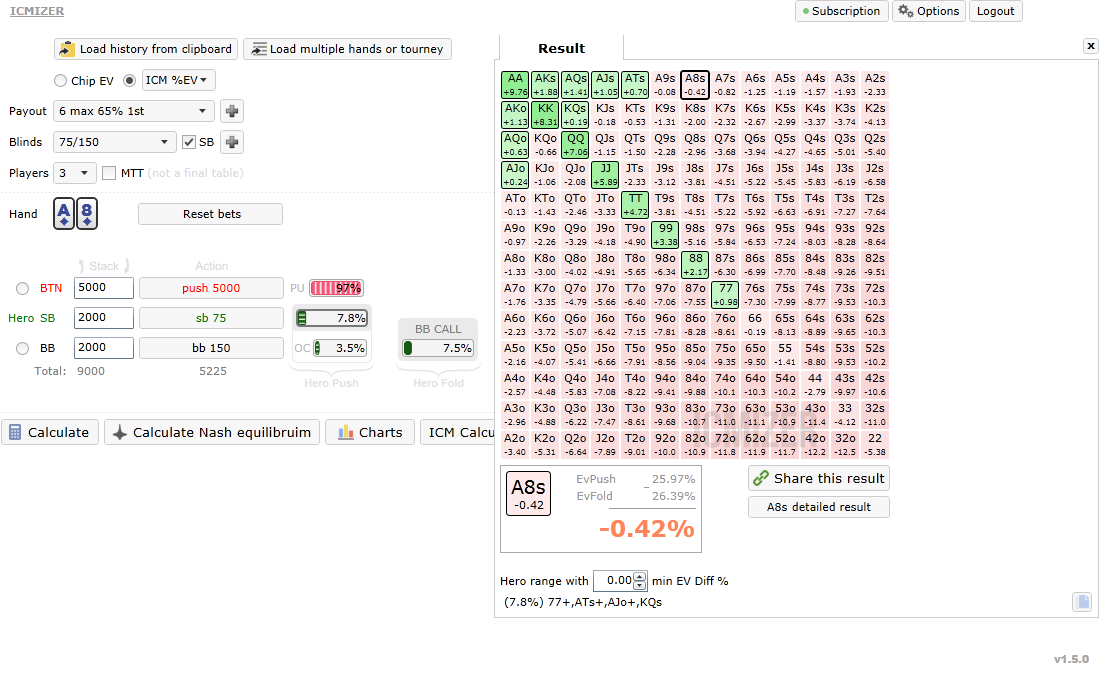
So I've kept all of the variables the same but tweaked the stack sizes.
And as you can see, we can actually call off wider and AQo a fold before is now a call. According to ICMIZER, the range we can profitably call off with is 7.8% - that's A-Jo+/A-10s+/KQs/7s+. That may surprise some of you – the fact we have more blinds and yet call off wider, but it's simply down to the equity gain. In this situation, if we collide with and eliminate the short stack our equity increases from 26.39% to 48.33% and if we collide with the big stack and win our equity increases from 26.39% to 42.22% so clearly it’s better for our equity to tangle with the short stack. However, unlike in the first situation, if we collide with and beat the big stack we’ll gain the majority of chips in play thus taking the big stack and so will have decent equity. This should put us in a nice commanding position and increase our chance of a 1st place finish, whereas doubling up in scenario one doesn’t increase our chance of a 1st place finish by any means. If the remaining players know ICM this will also let us use our big stack to its potential, although it should still be reinforced we should never deviate from ICM here and call wider because our priority still lies with colliding with the other short stacked opponent.
Of course, in this situation, it's not practical an opponent on the BTN here would jam 97% into 2 opponents for an effective 13.33bbs; the Nash equilibrium range in this spot is 47% but all the same, it's also not practical an opponent would jam some of the top hands in their range like As/AKo/AQo – those hands would most certainly induce for value whereas in situation one some top regs may jam some of those hands to range balance, particularly if they were doing a lot of pushing. If we estimate our opponent is pushing as wide as the Nash range in this spot but assuming they'll induce the top 7% of hands – A-Jo+/A-10ss+/9s+ giving them an overall push range of around 40% of cards (7%-47%), we can call off with 8% of cards which is A-10o+/A-10ss+/8s+. This range is still wider than what we could call off with when we had 1.25k chips even though our opponent has 57% fewer cards in his range, albeit that includes the top 7%.
Conclusions
Concluding, the moral of the story is never kiss goodbye to your tournament equity or write off your chances of cashing when you're short stacked on the bubble. Although sometimes you'll have no choice but to collide with the big stack, your goal should be to collide with the player whose chips are worth the most amount of $ to you and in both examples demonstrated, that's clearly the other opponent in the blinds!
It's important to remember you must call the big stack tighter when you're even short stacked with another opponent on the bubble (i.e. 6k-1.5k-1.5k stacks) vs being a clear short stack (i.e. 4.5k-3k-1.5k stacks) since you have more equity to protect as you aren't as distant from the money/favourite to bubble so even though your stack size is the same in each case the range for calling off always varies based on stack size fluctuations. It seems some players are ignoring some of these important principles and abandoning ICM when in possess of a short stack on the bubble and to do so is simply leaving $ at the tables.
Live long and prosper
MikeyMcD45
Related articles
• Super short stacked pushing tactics on the bubble