Formulas to calculate equity
“How much equity do I need to make the call” is a common question asked in various tournament spots. Correct formulas, which answer this question and discussion of mistake in popular but simplified approach to this poker problem in this article.
In tournament spot we choose call over fold when our ICM EV of Call is greater than ICM EV of fold.
The correct calculation formula is
Hand win% × ICM EV win + Hand tie% × ICM EV tie + Hand lose% × ICM EV lose > ICM EV fold (1)
If we aren’t in the money yet formula can be simplified to
Hand win% × ICM EV of win + Hand tie% × ICM EV of tie > ICM EV of fold(1 simplified)
It still includes both win% and tie%, and doesn’t include hand equity. Hand equity formula is :
equity% = win% + (tie% / 2)
Incorrect formula is based on this equity% and is
Hand equity% × ICM EV of win + (100 - equity%) × ICM EV of lose > ICM EV of fold
If lose scenario doesn’t grant us any payout and ICM EV of lose is 0% it can be simplified to
equity% × ICM EV of win > ICM EV of fold (2)
It can be rewritten as equity% > ICM EV of fold / ICM EV of win (3)
Last formula is very simple to use and has practical value. All you need to know is EV fold and EV of win vs. pushing player. You can then quickly get an idea of your required equity.
Analyzing heads up or cash scenarios
Earlier I said that formula 1 is correct and formula 2 is wrong. It is true for tournament poker situation where there are more than 2 players and payout structure contains different payouts. However in cash or heads up both formulas are correct.
Consider following HU scenario
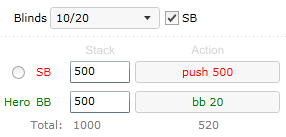
Small blind pushes, we are on the BB. We can calculate outcomes EV in chips because payout doesn’t matter.
We complete first formula with values
Hand win% × 1000 + Hand tie% × 500 + Hand lose% × 0 > 480, or
Hand win% × 1000 + Hand tie% × 500 > 480
If we win more than 48% of the time it is worth the call, regardless of our chance to tie.
Simplified formula will look like
equity% × 1000 > 480
We will analyze sample scenario and calculate EV of push (left part) if hero hand versus opponent range wins 45% of the time and ties 10% of the time. According to equity formula hero will have 50% equity with such hand.
Hand win% × 1000 + Hand tie% × 500 then becomes
0.45 × 1000 +0.1 × 500 = 500 chips
equity% × 1000 then becomes
0.5 × 1000 = 500 chips
Both formulas produce same result, so we can use a simple formula for analysis of such poker hands.
Analyzing tournament scenarios with ICM effect
Both formulas produced the same results in HU scenario, but in tournament scenario with ICM effect in place they will not, and second formula will prove to be wrong.
Consider following 3 way scenario in tournament with 6 max payout.
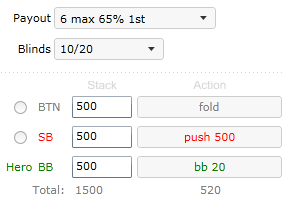
Again small blind pushes 500 chips, but now our equity has to be calculated with ICM.
So our ICM EVs are: ICM EV win 55%, ICM EV tie 33%, ICM EV lose 0%
Note that double up doesn’t double up our ICM equity, it should have been 66% but actual value is only 55% of prize pool. This is so called nonlinear ICM effect at work.
It should be clear that formulas will produce different results now. Again we assume our hand wins 45% of the time and ties 10% of the time.
We calculate Push EV based on formula (1): 0.45 × 55% + 0.1 × 33% = 28.05%
Push EV based on formula (2) will be: 0.5 × 55% = 27.5%
Note that first formula produced greater value than second formula, so we could actually have smaller equity than 50% and still have greater EV than EV calculated by wrong formula 2.
So you will get tighter call ranges if you try to calculate your calling range in this spots based on equity based formula, which would be wrong.
Applying formulas for actual hands and ranges
Second formula is very popular, partly because programs like Sng Wizard perform calculations based on it, and ignore existence of tie scenarios. Let us analyze a hypothetical bubble scenario of 9 max sit and go.
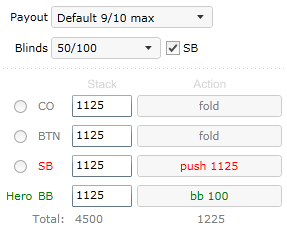
Hero is BB and SB pushes. How much equity do we need to make the call? We will use the incorrect second formula for this example.
ICM expected values for potential outcomes are: EV Fold 23.53%, EV Win 38.33%, EV lose 0%
We enter them in formula (3) and get
equity% > ICM EV of fold / ICM EV of win or equity% > 23.53 / 38.33 × 100% or equity% > 61.39%
61% equity is a lot. And it would mean that we have to be very tight in this particular spot, if the formula was correct.
What if I told you that we could have a very healthy +EV call and we actually only hand 50% of equity in this spot, 11% less and generally a far more achievable value.
You probably wouldn’t believe it. After all formula is technically wrong, but can it make a mistake of 11% equity? It can indeed. Please check following calculation:
http://www.icmpoker.com/icmizer/#YYaZ
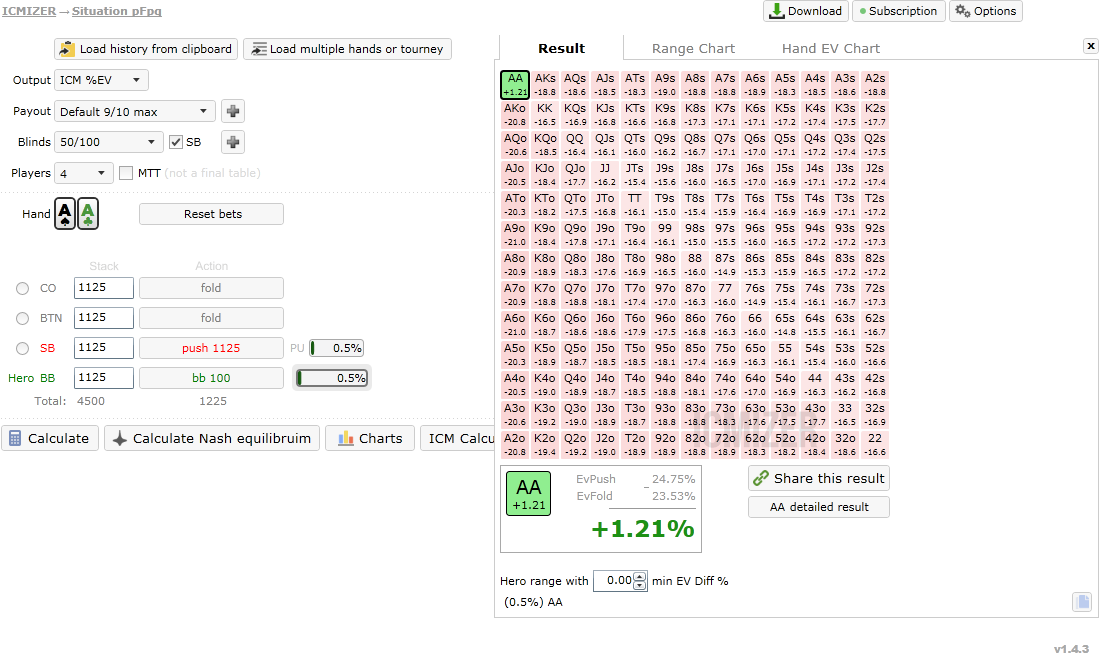
Aces have exactly 50% equity versus opponent’s aces. However we should make this call with only 50% equity, which is far behind previously calculated 61%.
To see how it was possible we should use correct formula (1).
Again, ICM expected values for potential outcomes are: EV Fold 23.53%, EV Win 38.33%, EV tie 25%
AA wins against AA 2.17% of the time, and splits the pot 95.65% of the time.
So, Hand win% × ICM EV of win + Hand tie% × ICM EV of tie + Hand lose% × ICM EV of lose > ICM EV of fold becomes
2.17% × 38.33% + 95.65% × 25% + 2.17% × 0% > 23.53% or
24.75% > 23.53%
Note that if you try this scenario hand in Sng Wizard you will see that it uses wrong formula, and It will incorrectly suggest you to fold, because you do not have that desired 61% equity with aces here.
ICMIZER on the other hand uses more precise formulas and provides correct results.
Conclusion
While second formula is wrong, it can be used to get an idea of hands which are definitely worth the call. But it will ignore hands, which didn’t have enough equity, but were also +EV call hands and shouldn’t be folded in such spots.
You can also use simplified formula in heads up or cash spots, where you can calculate required equity on the fly after some practice.