In some types of tournament spots, it can be considerably harder to make the correct decision than in others.
What should we take into consideration in order to figure out whether we should push our hand or fold it? We need to plug the tournament spot into ICMIZER, and then assign ranges to our opponents and hit the "Calculate" button. The problem is: it is impossible to precisely predict opponent’s ranges. When we are predicting or estimating range for opponent we can usually rely on 3 things: our experience, Nash equilibrium ranges for our current spot, and luck.
In the context of this article, I will be calling spots difficult if luck (3rd factor) plays a much bigger role in this prediction than in typical tournament spots.
Let's jump into our first example:
http://www.icmpoker.com/icmizer/#mzen
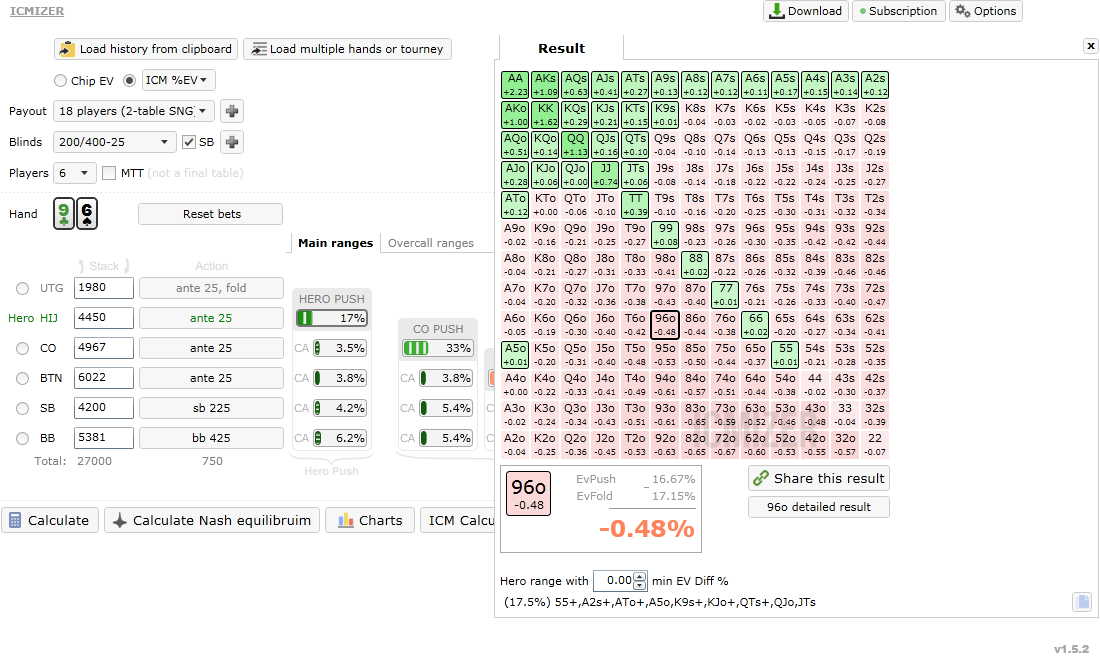
Let's look at a pretty typical 18 man tournament spot: 6 players are remaining, and
we are close to the money.
We are in the HIJ position (or UTG+1 for a 6 way spot). Ranges are assigned, and we can see that ICMIZER calculated that 17.5% hands should be pushed in this spot.
Now let's make a minimal change to a single range: we remove TT from the big blind's
calling range. As a result, we can see that our pushing range has jumped to 27% of
hands!
http://www.icmpoker.com/icmizer/#IqNn
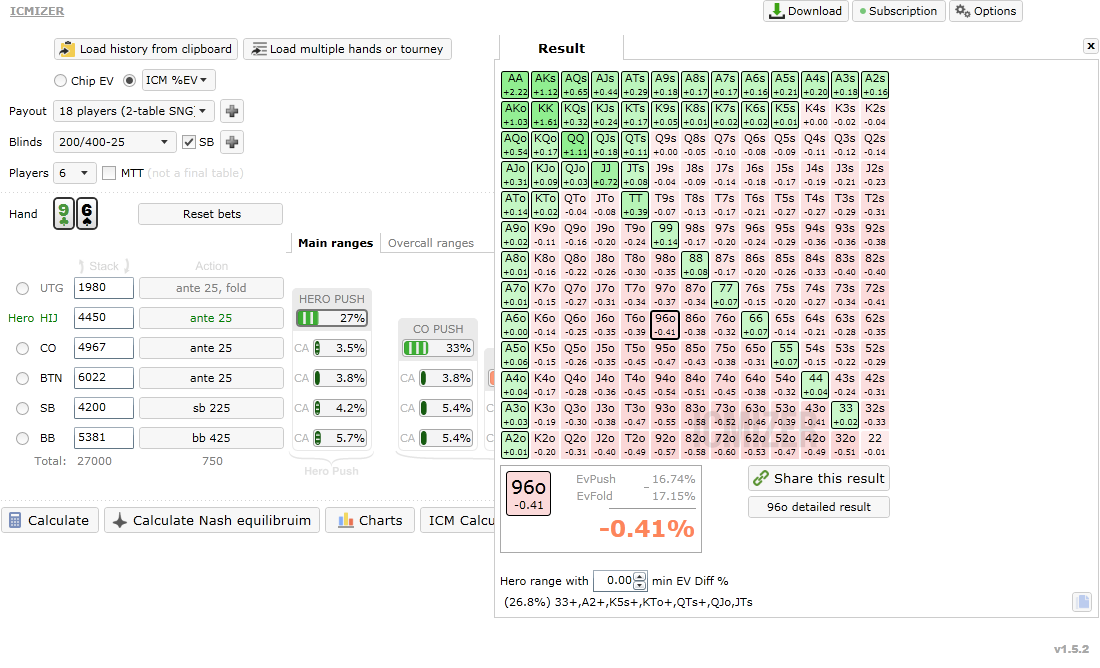
Percentage-wise, this is more than a 50% increase in our pushing range. So what are we supposed to do in this situation with hands that fall within the difference between these two ranges? We can't be 100% certain in how accurately we are able to estimate opponent ranges. Further, we aren’t certain that players are going to limit themselves to just push or fold decisions, and that they will not attempt to pull off a minraise
or limp move. It’s difficult to determine how to take into account the chance that they might actually deviate from a preflop push-fold strategy, when we are trying to figure
out what to do with a hand like A7o or KTo.
We are in a precarious spot. No one can predict an opponent's call ranges in this spot to +/- 2% precision, not to mention a precision of 0.45% (which is the chance of being dealt TT preflop). As long as we didn’t miss something big somewhere in our range prediction, it seems that push or fold with those hands can’t possibly be
considered a big mistake. It's unlikely that a more experienced player would be able to
get a much better idea in this spot and avoid the mistake, or to be certain that he/she
is making the correct decision. Even a high stakes poker professional won’t be able to say precisely how opponents will play in this spot, and to answer with certainty whether we should push A7o in this spot.
However a poker professional will be able to play better in simpler scenarios. In scenarios where the pushing range dependency on our range prediction precision is not so strong, which luckily are a majority of tournament spots. We can be much more certain in those kinds of poker tournament spots. It means we can outplay our opponents in them - as long as we are doing our push/fold homework and they aren’t.
Characteristics of difficult spots
- Tight calling ranges of our opponents
- Big ICM pressure on players (bubble is close)
If tournament spots meet these conditions, then the following things get noticeably more difficult: finding a Nash equilibrium approximation; and making the correct
decision with strong, but not premium hands, which fall in that “in between” zone,
described earlier.
What is so challenging about finding Nash equilibrium in this kind of spots? As we
saw earlier, a single hand being removed from a range significantly impacted our
pushing range. This not only means that finding a Nash equilibrium approximation will
be difficult. It also means that once we determine a Nash equilibrium ranges solution,
we will find it to have less stability than Nash equilibrium solutions for spots which
do not meet these two criteria.
By stability of Nash equilibrium in this situation, I mean the following: after
finding Nash equilibrium ranges in ICMIZER, we press the "Calculate" button. Stability
is low in cases where the calculated range is significantly different from the range
which came from the Nash equilibrium calculation. Smaller differences mean greater
stability.
Here I should point out that ICMIZER doesn’t find the ideal Nash equilibrium, but
rather it finds the Nash equilibrium approximation which is closest to the ideal Nash equilibrium. We are talking about the stability of this approximation. If actual Nash equilibrium existed, it would be stable by definition of Nash equilibrium - however,
it usually doesn’t exist, and so therefore we are dealing with approximations.
When ICMIZER analyzes ranges or finds Nash equilibrium, it considers that players
will either play a hand or they won't. From an ICMIZER perspective, he/she cannot push
A5o in 87% of cases, and fold it other 13% of cases. This kind of range “integrity” corresponds to reality: your opponents aren’t likely to sit with D100 dice and fold A5o if they get less than 13 on their roll. Our real world players either play a hand or they fold it.
It is important to understand that if we would be using ranges, which would assume
that opponents could play some hands in their ranges sometimes, we could increase
the stability of our Nash equilibrium approximations. However, we would really be
talking about purely theoretical results because real world poker players aren’t only
sometimes playing hands in their usual daily pushing or calling ranges.
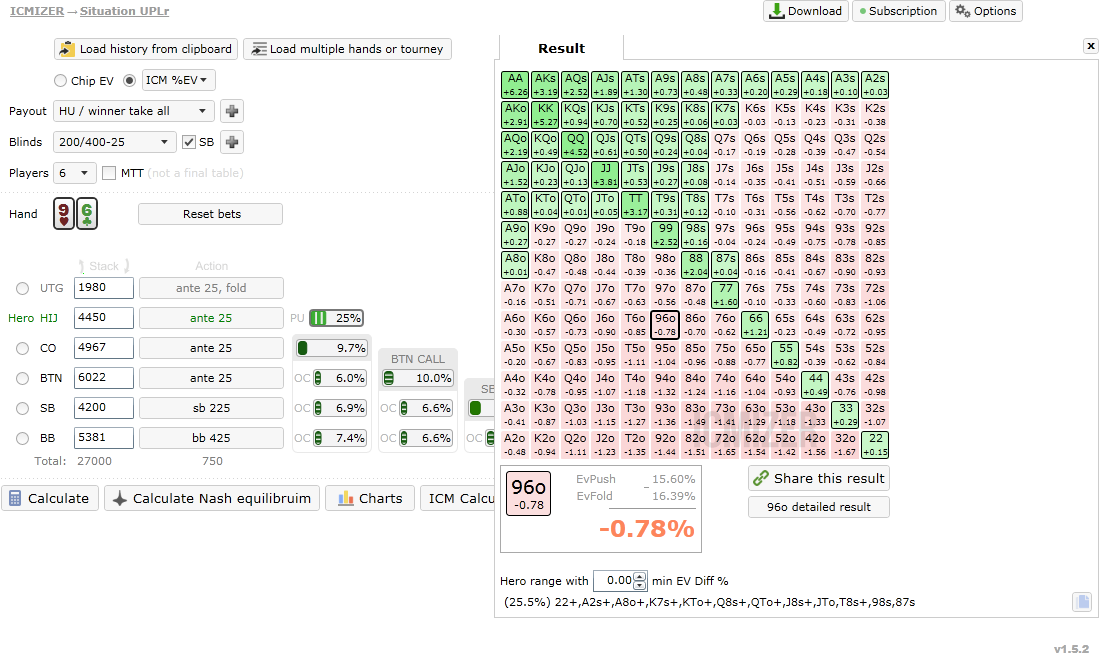
Now we will compare the difficult spot from our example with a simpler one.
When we find Nash equilibrium, we get a pushing range for HIJ equal to 18%. When we
hit the "Calculate" button, we can see that it changes to 14% of hands, which is a
relatively big difference.
Let's now change the payout structure to a less strict one, for example "Winner take
all", and leave everything else intact. We can see that Nash equilibrium range is now
24%, and after we hit the "Calculate" button it changes to 25%. The change is smaller
both in absolute and relative terms.
http://www.icmpoker.com/icmizer/#TNGv
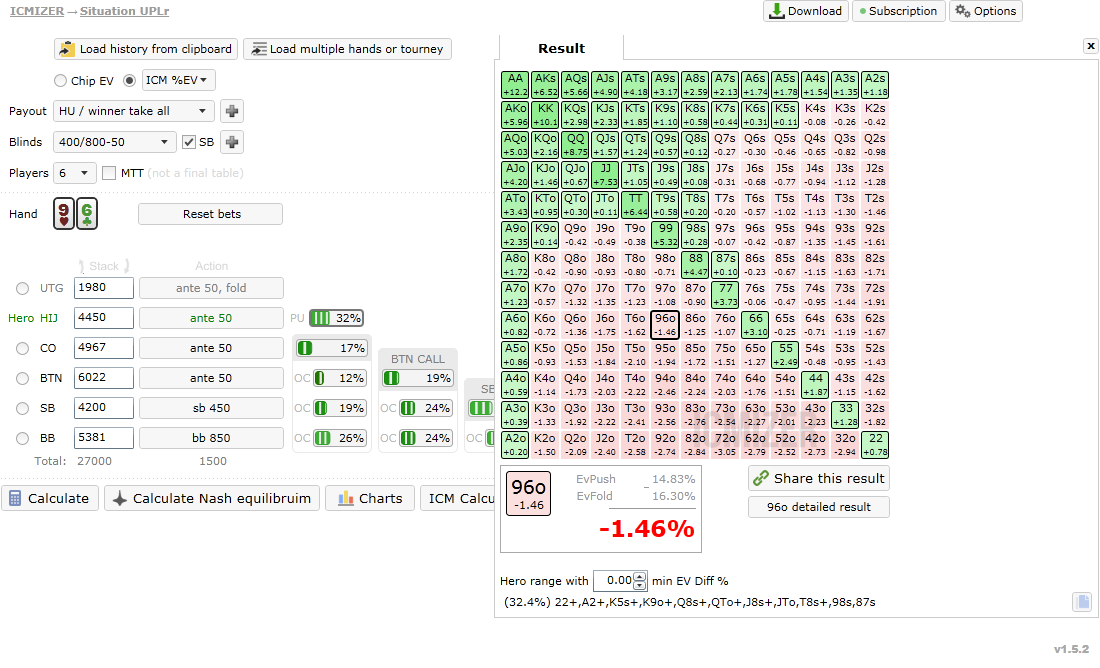
In addition to the payout structure change, let's shorten up the stack depth by
doubling the blinds. Now we can see that Nash equilibrium suggests pushing 32% of hands,
and when we hit the "Calculate" button, the range remains at 32%. Stability is even
higher in this case. This is a result of wider calling ranges in shorter stack
conditions.
http://www.icmpoker.com/icmizer/#KuVT
I hope this article will help you to better understand the specifics of ICM
calculations and how to apply this knowledge in your game. This article is a result of
some hot forum discussion, and I would be glad to see some comments to it too.
Q
You might also like:
Video: Nash calculator video by Q
Article: The Nash Calculator and the Nash Equilibrium strategy in poker, by MikeyMcD45